9  Time Series Regression with Correlated Errors

The goal of this lecture is to bring together knowledge about regression, time series trends, and autocorrelation with the goal of obtaining correct inference in regression problems involving time series. You should become capable of suggesting a model that would meet the goal of data analysis (testing certain relationships) while satisfying assumptions (e.g., uncorrelatedness of residuals) and minimizing the risk of spurious results.

Objectives

  1. Model autocorrelated residuals (in other words, incorporate or account for autocorrelation) so the final residuals satisfy modeling assumptions.
  2. Apply and interpret Granger causality that is based on time series predictability.

Reading materials

9.1 Introduction

Here we explore a regression model with autocorrelated residuals. We already know how to

  • forecast, construct prediction intervals, and test hypotheses about regression coefficients when the residuals satisfy the ordinary least squares (OLS) assumptions, i.e., the residuals are white noise and have a joint normal distribution \(N(0, \sigma^{2})\);
  • model serial dependence (i.e., autocorrelation) in stationary univariate time series, such as using ARMA models.

Here we bring these two skills together.

If the residuals do not satisfy the independence assumption, we can sometimes describe them in terms of a specific correlation model involving one or more new parameters and some ‘new residuals.’ These new residuals essentially satisfy the OLS assumptions and can replace the original correlated residuals (which we will sometimes call the ‘old’ residuals) in the model.

When modeling time series, we often want to find so-called leading indicators, i.e., exogenous variables whose lagged values can be used for predicting the response, so for the forecasts we do not need to predict \(X\)-variables that are employed in a model. Hence, our models may include lagged versions of both the response and predictor variables (a general form of such a model was given in Equation 2.2).

9.2 Cross-correlation function

Cross-correlation is a correlation between different time series, typically with a time offset \(k\) (a.k.a. lag): \[ \mathrm{cor}(X_{t+k},Y_t). \tag{9.1}\] (Recall that autocorrelation is also a correlation with a lag present, but for the same time series.) By calculating cross-correlations at each lag \(k = 0, \pm 1, \pm 2, \dots\), we obtain the cross-correlation function (CCF). CCF shows how the correlation coefficient varies with the lag \(k\) and helps us to identify important lags and find leading indicators for predictive models. For example, the relationship between nutrient input and algal blooms in a marine environment is not immediate since the algae need time to reproduce. The correlation between a time series of births and demand for baby formula would be distributed over smaller lags \(l\) \[ \mathrm{cor}(\mathrm{Births}_{t - l}, \mathrm{FormulaDemand}_t) \] than the correlation lags \(L\) between births and school enrollments \[ \mathrm{cor}(\mathrm{Births}_{t - L}, \mathrm{SchoolEnrollment}_t), \] where \(l,L > 0\) and \(l < L\).

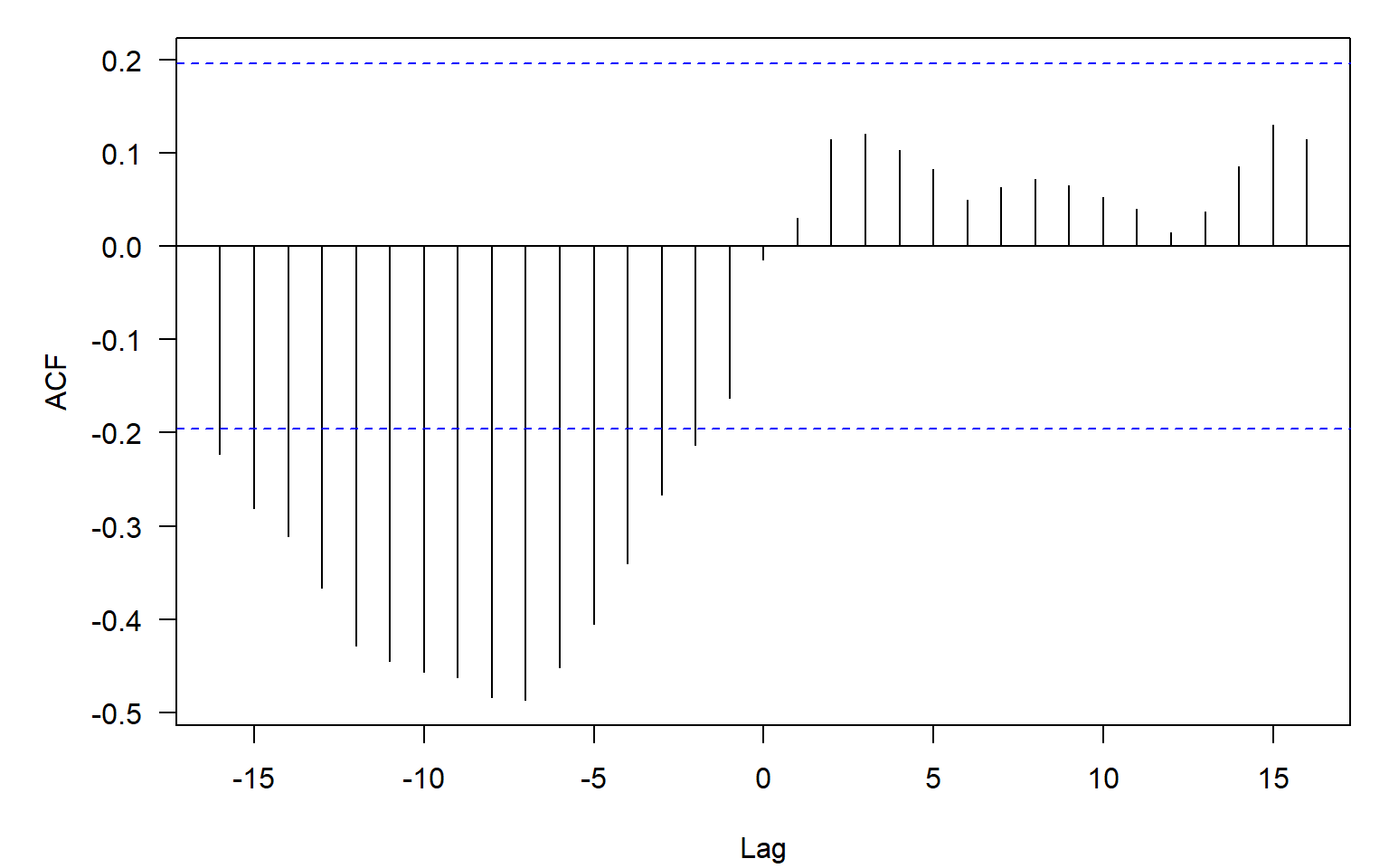
The functions ccf() and forecast::ggCcf() estimate the cross-correlation function and plot it as a base-R or a ggplot2 graph, respectively. The functions use the notations like in Equation 9.1, hence when using ccf(x, y) we are typically interested in identifying negative \(k\)s that correspond to correlation between past values of the predictor \(X_t\) and current values of the response \(Y_t\).

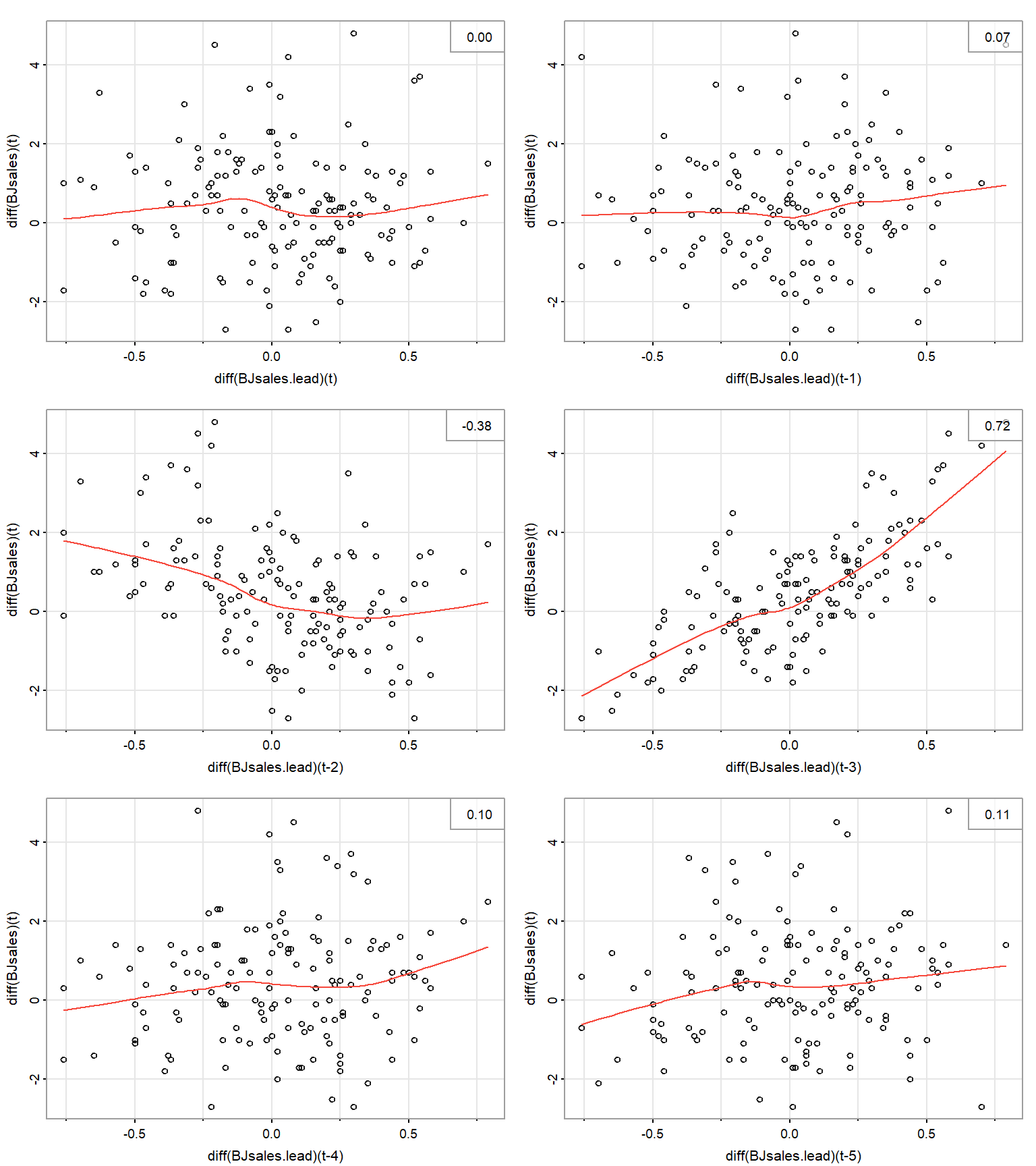
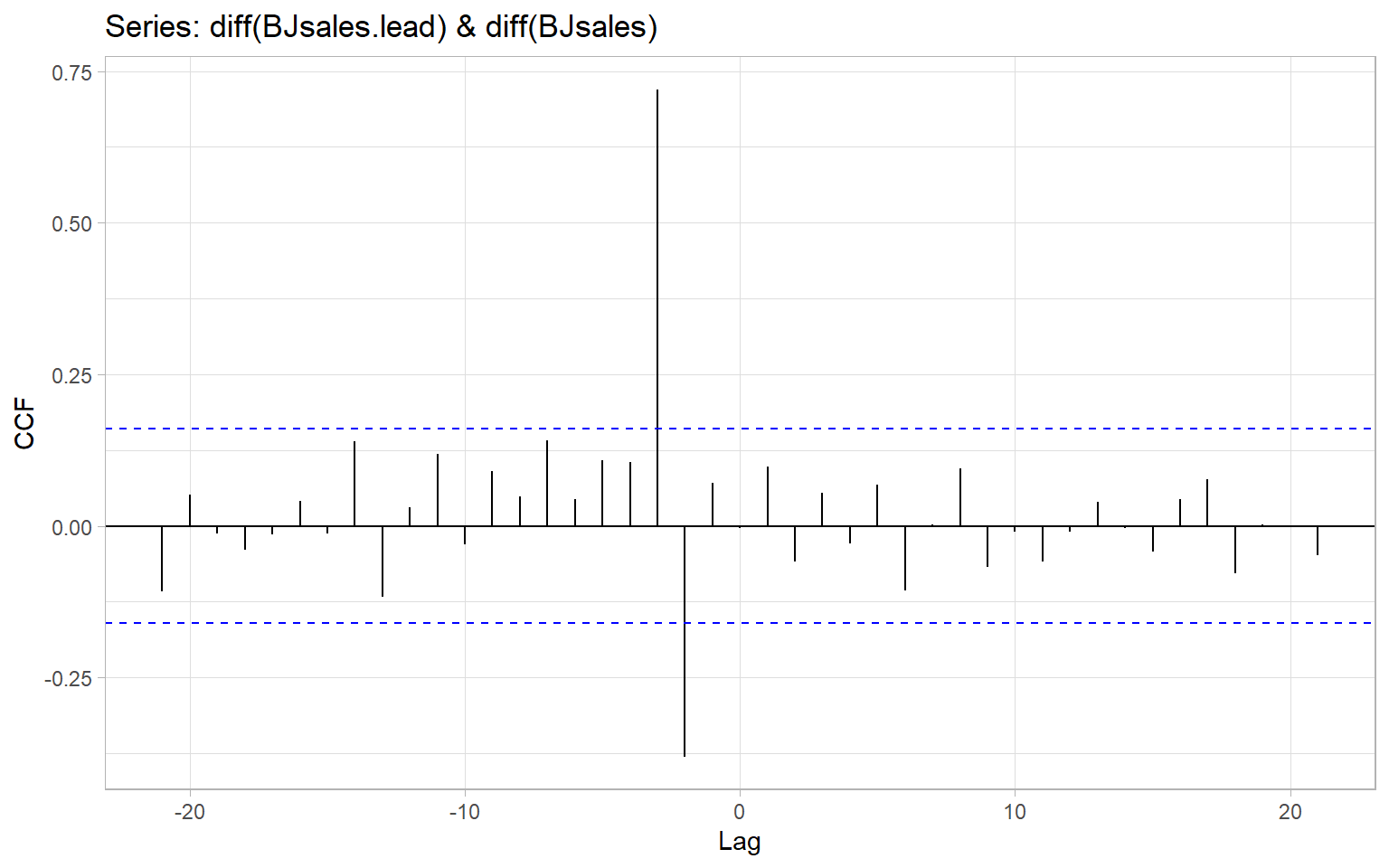
For example, Figure 9.1 shows the CCF for two time series of sales that have been detrended by taking differences. From this plot, lagged values of the first series, \(\Delta \mathrm{BJsales.lead}_{t - 2}\) and \(\Delta \mathrm{BJsales.lead}_{t - 3}\) are significantly correlated with current values of the second series, \(\Delta \mathrm{BJsales}_{t}\). Hence, we can call BJsales.lead a leading indicator for BJsales.

Code
forecast::ggCcf(diff(BJsales.lead), diff(BJsales))

Figure 9.1: Cross-correlation function of the detrended time series.

Note

The function ccf() assumes that the two time series are evenly spaced and have no missing data. We can use the argument na.action = na.pass to ignore any missing values.

Note that the 95% confidence band shown in Figure 9.1 is based on how i.i.d. series of length \(n\) would correlate (the same way the band is produced for an autocorrelation function with acf()). However, when \(n\) is small, there are not so many pairs \((X_{t+k}, Y_t)\) to calculate the correlations at large lags, hence the confidence bands should be adjusted by using the smaller \(n'(k) = n - |k|\) to account for this lack of confidence.

Another concern is the autocorrelation of individual time series that may lead to spurious cross-correlation (Dean and Dunsmuir 2016). Intuitively, say if \(X_t\) and \(Y_t\) are independent from each other but both \(X_t\) and \(Y_t\) are positively autocorrelated – high (or low) values in \(X_t\) follow each other, and high (or low) values in \(Y_t\) follow each other – there could be a time alignment among our considered lags \(k = 0, \pm 1, \pm 2, \dots\) when the ups (or downs) in \(X_{t+k}\) match those in \(Y_t\). This may result in spurious cross-correlation. To address the concern of autocorrelation, we can apply bootstrapping to approximate the distribution of cross-correlation coefficients corresponding not to the i.i.d. series but to stationary time series with the same autocorrelation structure as the input data. The function funtimes::ccf_boot() implements the sieve bootstrap and returns results for both Pearson and Spearman correlations (Figure 9.2).

Code
set.seed(123)
res <- funtimes::ccf_boot(diff(BJsales.lead), diff(BJsales), 
                          B = 10000, plot = "none")
p1 <- res %>% 
    ggplot(aes(x = Lag, y = r_P, xend = Lag, yend = 0)) + 
    geom_ribbon(aes(ymin = lower_P, ymax = upper_P), fill = 4) +
    geom_point() + 
    geom_segment() + 
    geom_hline(yintercept = 0) + 
    ylab("Pearson correlation")
p2 <- res %>% 
    ggplot(aes(x = Lag, y = r_S, xend = Lag, yend = 0)) + 
    geom_ribbon(aes(ymin = lower_S, ymax = upper_S), fill = 4) +
    geom_point() + 
    geom_segment() + 
    geom_hline(yintercept = 0) + 
    ylab("Spearman correlation")
p1 + p2 +
    plot_annotation(tag_levels = 'A')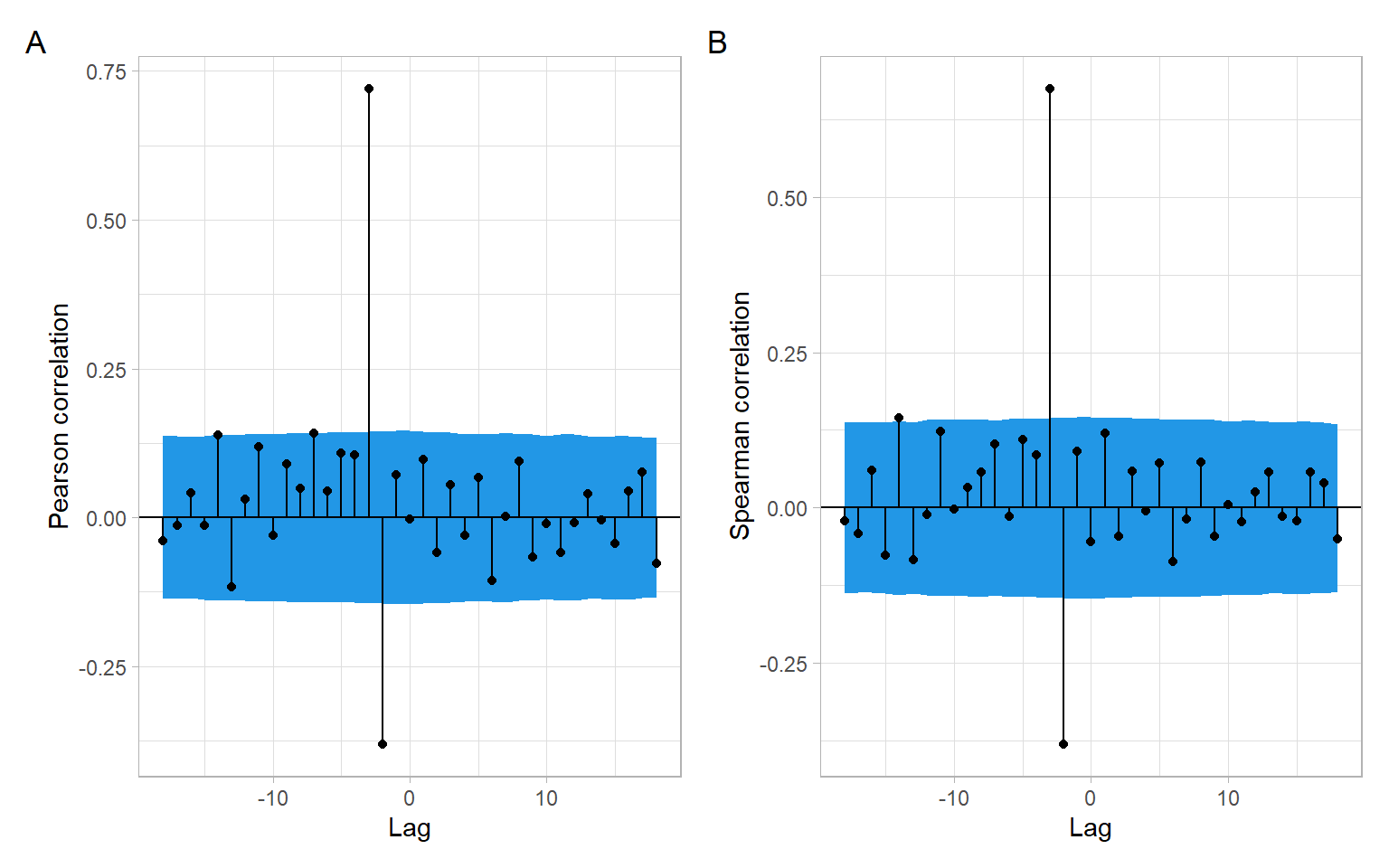

Figure 9.2: Pearson and Spearman cross-correlation functions of the detrended time series with sieve bootstrap confidence intervals. Note that the function funtimes::ccf_boot() automatically produces a base-R plot that was suppressed here to save the results as the object res and use the package ggplot2 for the plots.

Finally, remember that the reported Pearson correlations in Figure 9.1 and Figure 9.2 A measure the direction and strength of linear relationships, while Spearman correlations in Figure 9.2 B correspond to monotonic relationships. To further investigate whether the lagged relationships are linear, monotonic, or of some other form, we need to plot the lagged scatterplots (Figure 9.3). Also see other functions in the package astsa, such as the function astsa::lag1.plot() for exploring nonlinear autocorrelations.

Code
astsa::lag2.plot(diff(BJsales.lead), diff(BJsales), max.lag = 5)

Figure 9.3: Lagged scatterplots of the detrended time series with lowess smooths and (linear) Pearson correlations reported in the right corners.

9.3 Linear regression with ARMA errors

We begin with the simplest case, a constant mean model, where the residuals are serially correlated and follow an AR(1) model, that is \[ Y_{t} = \beta_{0} + \epsilon_{t}, \tag{9.2}\] where \(\epsilon_{t} \sim\) AR(1), i.e., \[ \epsilon_{t} = \phi \epsilon_{t - 1} + a_{t}. \tag{9.3}\]

Here \(\phi\) is a real number satisfying \(0 < |\phi| < 1\); \(a_{t}\) is white noise with zero mean and the variance \(\nu^{2}\), i.e., \(a_{t} \sim \mathrm{WN}(0,\nu^2)\). We also assume that \(\mathrm{cov}(a_{t}, \epsilon_{s}) = 0\) for all \(s < t\) (i.e., that the residuals \(\epsilon_s\) are not correlated with the future white noise \(a_t\)).

Equation 9.3 allows us to express Equation 9.2 as \[ Y_{t} = \beta_{0} + \phi \epsilon_{t - 1} + a_{t}. \tag{9.4}\]

The advantage of this representation is that the new residuals \(a_{t}\) satisfy the OLS assumptions. In particular, since \(a_{t}\) is white noise, \(a_{t}\) is homoskedastic and uncorrelated.

We shall also assume that \(a_{t}\) are normally distributed (for justification of the construction of confidence intervals and prediction intervals). However, even if \(a_{t}\) are not normal, \(a_{t}\) are uncorrelated, which is a big improvement over the serially correlated \(\epsilon_{t}\).

Our goal is to remove the \(\epsilon_{t}\) entirely from the constant mean model and replace them with \(a_{t}\) acting as new residuals. This can be done as follows. First, write Equation 9.2 for \(t-1\) and multiply both sides by \(\phi\), \[ \phi Y_{t -1} = \phi \beta_{0} + \phi \epsilon_{t - 1}. \tag{9.5}\]

Taking the difference (Equation 9.4 minus Equation 9.5) eliminates \(\epsilon_{t}\) from the model: \[ \begin{split} Y_{t} - \phi Y_{t - 1} &= \left( \beta_{0} + \phi \epsilon_{t - 1} + a_{t} \right) - \left( \phi \beta_{0} + \phi \epsilon_{t - 1} \right) \\ &= (1 - \phi) \beta_{0} + a_{t}. \end{split} \]

Therefore we can rewrite the constant mean model in Equation 9.2 as \[ Y_{t} = (1 - \phi) \beta_{0} + \phi Y_{t - 1} + a_{t}. \tag{9.6}\]

In general, for any multiple linear regression \[ Y_{t} = \beta_{0} + \sum^{k}_{j =1} \beta_{j} X_{t,j} + \epsilon_{t}, ~~ \text{where} ~~ \epsilon_{t} \sim \mbox{AR(1)}, \tag{9.7}\] we can perform a similar procedure of eliminating \(\epsilon_{t}\).

This elimination procedure leads to the alternate expression \[ Y_{t} = (1 - \phi) \beta_{0} + \phi Y_{t -1} + \sum^{k}_{j = 1} \beta_{j} (X_{t,j} - \phi X_{t-1, j}) + a_{t}, \tag{9.8}\] where \(a_{t}\) is white noise, i.e., homoskedastic with constant (zero) mean and uncorrelated. See Appendix B describing the method of generalized least squares and an example of \(k=1\).

Note that rewriting the model in this way pulls the autocorrelation parameter for the old residuals, \(\phi\), into the regression part of the model. Thus there are now \(k + 2\) unknown regression parameters (\(\beta_{0}, \beta_{1}, \dots, \beta_{k}\), and \(\phi\)). The introduction of an additional parameter into the regression part of the model can be regarded as the price to be paid for extracting new residuals \(a_{t}\) that satisfy the OLS assumptions.

Note that the new residuals \(a_{t}\) have smaller variance than the \(\epsilon_{t}\). In fact, \[ \begin{split} \sigma^{2} & = \mbox{var} (\epsilon_{t} ) = \mbox{var} (\phi \epsilon_{t - 1} + a_{t}) \\ \\ & = \phi^{2} \mbox{var}(\epsilon_{t - 1}) + \mbox{var} (a_{t} ) ~~~ \mbox{since} ~~ \mbox{cov}(a_{t}, \epsilon_{t - 1}) = 0\\ \\ & = \phi^{2}\sigma^{2} + \nu^{2}, \end{split} \] leading to the relation \[ \nu^{2} = \sigma^{2} (1 - \phi^{2} ). \tag{9.9}\]

However, comparing Equation 9.6 with Equation 9.6, and Equation 9.8 with Equation 9.7, we see that the rewritten form of the model is not linear in terms of the parameters \(\beta_{0}, \beta_{1}, \dots, \beta_{k}\) and \(\phi\). For example, the intercept term \((1 - \phi) \beta_{0}\) involves a product of two of the parameters. This nonlinearity makes the OLS, implemented in the R functions lm() and lsfit(), a poor method for obtaining parameter estimates. Instead, we will use the method of maximum likelihood (ML) carried out through such R functions as arima().

The function arima() allows us to input the model in its original form, as in Equation 9.7. It then internally rewrites the model to put it in the form of Equation 9.8. (So we do not have to rewrite the model!) It then makes the assumption that the \(a_t\) are normal and constructs the multivariate normal likelihood function \[ L (Y_{1} , \dots , Y_{n}; Q ), \] where \(n\) is the sample size and \(Q\) is the vector of all unknown parameters. In general, for an AR(1) model with \(k\) original predictors, we have \(Q = (\phi, \beta_{0}, \beta_{1}, \dots, \beta_{k}, \nu^{2})\). Recall that \(\nu^{2} = \mathrm{var}(a_{t}) = \mathrm{cov}(a_{t} , a_{t})\).

The function arima() then uses the historical data \(Y_{1}, \dots, Y_{n}\) to find the parameter estimates \[ \hat{Q} = \left( \hat{\phi}, \hat{\beta}_{0} , \hat{\beta}_{1} , \dots, \hat{\beta}_{k} , \hat{\nu}^2 \right), \] which maximize the likelihood \(L\). These estimates (and other things, such as the standard errors of the estimates) can be saved to an output object in R. We will use an example to illustrate the use and interpretation of the function arima().

Moreover, we can extend the regression model in Equation 9.7 with AR(1) errors to a model with a more general form of errors, ARMA, by assuming \(\epsilon_t \sim \text{ARMA}(p,q)\) (see Chapter 6.6 in Brockwell and Davis 2002 and https://robjhyndman.com/hyndsight/arimax/): \[ \begin{split} Y_t &= \sum^{k}_{j =1} \beta_{j} X_{t,j} + \epsilon_{t},\\ \epsilon_{t} &= \phi_1 \epsilon_{t-1} + \dots + \phi_p \epsilon_{t-p} + \theta_1 a_{t-1} + \dots + \theta_q a_{t-q} + a_t. \end{split} \tag{9.10}\] This model in Equation 9.10 can be specified in R functions arima(), fable::ARIMA(), forecast::Arima(), and forecast::auto.arima().

Note

The R package forecast has been superseded by the new package fable that uses an alternate parameterization of constants, see ?fable::ARIMA.

Note

Remember that the variables \(Y_t\) and \(X_{t,j}\) (\(j = 1,\dots,k\)) should be detrended prior to the analysis (to avoid spurious regression results, see the previous lecture on dealing with trends in regression). If differencing is chosen as the method of detrending, the orders of differences \(d\) and \(D\) can be specified directly within the mentioned ARIMA functions (so R will do the differencing for us).

9.4 ARIMAX

ARIMAX (‘X’ stands for ‘external regressor’) models are closely related to Equation 9.10, but there is an important difference. For simplicity of notation, we can present an ARMAX(\(p,q\)) model that is a regular ARMA(\(p,q\)) model for \(Y_t\) plus the external regressors: \[ \begin{split} Y_t &= \phi_1 Y_{t-1} + \dots + \phi_p Y_{t-p} + \theta_1 a_{t-1} + \dots + \theta_q a_{t-q} + a_t\\ &+\sum^{k}_{j =1} \beta_{j} X_{t,j}, \end{split} \tag{9.11}\] where \(a_t\) is still a zero-mean white noise process. Interestingly, at this time there is no convenient way to estimate this model in R. One could manually write lagged values of \(Y_t\) as external regressors (i.e., create new variables in R for \(Y_{t-1},\dots, Y_{t-p}\)), use these variables in the R functions mentioned above, but force \(p=0\) (e.g., Soliman et al. 2019 used the functions from the R package forecast).

The difference between Equation 9.10 and Equation 9.11 is the presence of lagged values of the response variable, \(Y_t\), in Equation 9.11. As Hyndman points out, regression coefficients \(\beta_j\) in Equation 9.11 lose their interpretability compared with usual regression and do not show the effect on \(Y_t\) when \(X_t\) increased by one. Instead, \(\beta\)’s in ARMAX Equation 9.11 are interpreted conditional on the value of previous values of the response variable (https://robjhyndman.com/hyndsight/arimax/). Therefore, model formulation as in Equation 9.10 may be preferred.

Note

Other applicable models include models with mixed effects such as for repeated measures ANOVA (e.g., implemented in R using nlme::gls() and nlme::lme(), see different correlation structures; without a grouping factor, the results of nlme::lme(..., correlation = corARMA(...)) should be similar to estimating model in Equation 9.10). Other regression functions often borrow the functionality (and syntax) of the package nlme for estimating random effects, so autocorrelated residuals can be incorporated into a generalized additive model, GAM, mgcv::gamm(); generalized additive model for location scale and shape, GAMLSS, gamlss::gamlss(), which also can be used just as GAM, if scale and shape parameters are not modeled. A slightly different solution is possible using a generalized autoregressive moving average model (GARMA) demonstrated in Section 9.5, see gamlss.util::garmaFit().

Example: Golden tilefish ARIMAX

Here we have time series of 1918–2017 annual landings of golden tilefish (tonne) in the U.S. North Atlantic region and the Atlantic Multi-decadal Oscillation (AMO) index characterizing climatic conditions (Figure 9.4). These time series were described in Nesslage et al. (2021) with R code by Lyubchich and Nesslage (2020). The goal is to develop a regression model to explore the relationship between the landings and AMO.

Code
D <- read.csv("data/tilefish.csv")
summary(D)
#>       Year         Landings         AMO        
#>  Min.   :1918   Min.   :   5   Min.   :-0.434  
#>  1st Qu.:1943   1st Qu.: 454   1st Qu.:-0.148  
#>  Median :1968   Median : 749   Median : 0.014  
#>  Mean   :1968   Mean   : 952   Mean   : 0.001  
#>  3rd Qu.:1992   3rd Qu.:1204   3rd Qu.: 0.149  
#>  Max.   :2017   Max.   :3968   Max.   : 0.358  
#>                 NA's   :3
Code
p1 <- ggplot(D, aes(x = Year, y = Landings)) +
    geom_line() +
    xlab("Year") +
    ylab("Landings (tonne)")
p2 <- ggplot(D, aes(x = Year, y = AMO)) +
    geom_line() +
    xlab("Year") +
    ylab("AMO")
p1 + p2 +
    plot_annotation(tag_levels = 'A')

Figure 9.4: Time series plots of the golden tilefish landings and AMO.

Interpolation of missing data (a.k.a. imputation) is a separate and very expansive topic. For a univariate time series, linear interpolation can be implemented using forecast::na.interp(). Also, the landings time series required a power transformation, so the square root transformation was applied (Figure 9.5).

Code
D <- D %>% 
    mutate(Landings_noNA = as.numeric(forecast::na.interp(D$Landings))) %>% 
    mutate(Landings_noNA_sqrt = sqrt(Landings_noNA))

D %>% 
    dplyr::select(AMO, Landings_noNA_sqrt) %>% 
    GGally::ggpairs()

Figure 9.5: Scatterplot matrix of landings and AMO.

Code
par(mar = c(4, 5, 1, 1) + 0.1, mgp = c(3, 1, 0), mfrow = c(1, 1))
with(D,
     ccf(AMO, Landings_noNA_sqrt, las = 1)
)

Figure 9.6: Estimated cross-correlation function (CCF) of time series of the landings and AMO.

Based on the strongest lagged correlations (Figure 9.6), implement a model \[ \sqrt{Landings_t} = \beta_0 + \beta_{1} AMO_{t-7} + \epsilon_{t}, \] where \(\epsilon_{t} \sim\) ARMA(\(p,q\)), and the orders \(p\) and \(q\) are selected automatically based on Akaike information criterion.

Code
library(fable)
m1 <- D %>% 
    select(Year, Landings_noNA_sqrt, AMO) %>% 
    as_tsibble(index = Year) %>% 
    model(ARIMA(Landings_noNA_sqrt ~ dplyr::lag(AMO, 7)))

report(m1)
#> Series: Landings_noNA_sqrt 
#> Model: LM w/ ARIMA(2,0,0) errors 
#> 
#> Coefficients:
#>         ar1     ar2  dplyr::lag(AMO, 7)  intercept
#>       0.991  -0.184               -6.30       28.3
#> s.e.  0.104   0.102                5.02        3.4
#> 
#> sigma^2 estimated as 41.61:  log likelihood=-307
#> AIC=625   AICc=626   BIC=638

We forgot to check the stationarity of the time series! It seems that the landings can be considered as a unit-root process, so differencing is needed, hence a modified model is

\[ \Delta \sqrt{Landings_t} = \beta_0 + \beta_{1} AMO_{t-7} + \epsilon_{t}. \]

Code
m2 <- forecast::auto.arima(diff(D$Landings_noNA_sqrt),
                 xreg = dplyr::lag(D$AMO, 7)[-1],
                 allowmean = TRUE)
m2
#> Series: diff(D$Landings_noNA_sqrt) 
#> Regression with ARIMA(0,0,0) errors 
#> 
#> Coefficients:
#>        xreg
#>       -2.58
#> s.e.   3.82
#> 
#> sigma^2 = 46.3:  log likelihood = -313
#> AIC=629   AICc=630   BIC=634

Note it is different from the implementation with d = 1, which differences all the series.

\[ \Delta \sqrt{Landings_t} = \beta_0 + \beta_{1} \Delta AMO_{t-7} + \epsilon_{t} \]

Code
forecast::auto.arima(D$Landings_noNA_sqrt,
                     xreg = dplyr::lag(D$AMO, 7), 
                     d = 1)
#> Series: D$Landings_noNA_sqrt 
#> Regression with ARIMA(0,1,0) errors 
#> 
#> Coefficients:
#>        xreg
#>       -5.37
#> s.e.   5.14
#> 
#> sigma^2 = 45.7:  log likelihood = -309
#> AIC=623   AICc=623   BIC=628

Similarly, using the newer package fable.

Code
m3 <- D %>% 
    select(Year, Landings_noNA_sqrt, AMO) %>% 
    as_tsibble(index = Year) %>% 
    model(ARIMA(Landings_noNA_sqrt ~ pdq(d = 1) + dplyr::lag(AMO, 7)))

report(m3)
#> Series: Landings_noNA_sqrt 
#> Model: LM w/ ARIMA(0,1,0) errors 
#> 
#> Coefficients:
#>       dplyr::lag(AMO, 7)
#>                    -5.37
#> s.e.                5.14
#> 
#> sigma^2 estimated as 45.73:  log likelihood=-309
#> AIC=623   AICc=623   BIC=628

9.5 GARMA

Let \(Y_t\) be the observed time series and \(\boldsymbol{X_t}\) exogenous regressors. Then, we can model the conditional distribution of \(Y_t\), given \(Y_1,\dots,Y_{t-1}\), \(\boldsymbol{X_1,\dots,X_{t}}\) as \[ g(\mu_t)=\boldsymbol{X}'_t\beta+\sum_{j=1}^p\phi_j\{g(Y_{t-j})- \boldsymbol{X}'_{t-j}\beta\} +\sum_{j=1}^q\theta_j \{g(Y_{t-j})-g(\mu_{t-j})\}, \tag{9.12}\] where \(g(\cdot)\) is an appropriate link function; \(\mu_t\) is a conditional mean of the dependent variable; \(\boldsymbol{\beta}\) is a vector of regression coefficients; \(\phi_j\), \(j=1,\dots, p\), are the autoregressive coefficients; \(\theta_j\), \(j=1,\dots,q\), are the moving average coefficients, while \(p\) and \(q\) are the autoregressive and moving average orders, respectively.

In certain cases, the function \(g(\cdot)\) requires some transformation of the original series \(Y_{t-j}\) to avoid the non-existence of \(g(Y_{t-j})\) (Benjamin et al. 2003).

The generalized autoregressive moving average model (Equation 9.12), GARMA(\(p,q\)), represents a flexible observation-driven modification of the classical Box–Jenkins methodology and GLMs for integer-valued time series. GARMA further advances the classical Gaussian ARMA model to a case where the distribution of the dependent variable is not only non-Gaussian but can be discrete. The dependent variable is assumed to belong to a conditional exponential family distribution given the past information of the process and thus the GARMA can be used to model a variety of discrete distributions (Benjamin et al. 2003). The GARMA model also extends the work of Zeger and Qaqish (1988), who proposed an autoregressive exponential family model, and Li (1994), who introduced its moving average counterpart.

Example: Insurance claims GARMA model

Consider the weekly number of house insurance claims related to water and weather damage in one Canadian city. The number is standardized by the daily number of insured properties in that city. Explore the relationship between the number of claims and weekly total precipitation (mm).

Code
Insurance <- read.csv("data/insurance_weekly.csv") %>%
    dplyr::select(Claims, Precipitation)
summary(Insurance)
#>      Claims      Precipitation 
#>  Min.   :  0.0   Min.   : 0.0  
#>  1st Qu.:  1.0   1st Qu.: 0.8  
#>  Median :  3.0   Median : 3.8  
#>  Mean   :  3.6   Mean   : 7.7  
#>  3rd Qu.:  4.0   3rd Qu.:10.0  
#>  Max.   :170.0   Max.   :77.3
Code
Insurance %>%
    GGally::ggpairs()

Figure 9.7: Scatterplot matrix of weekly weather-related home insurance outcomes and precipitation.

Based on the distribution plots in Figure 9.7, the data are highly right-skewed (have heavy right tails). The number of claims is also a discrete variable. Therefore, we deal with non-normal distributions and need to use generalized-type models, like the generalized linear or additive models (GLMs or GAMs). Since there are many zeros in the counts of claims, we can start with the zero-adjusted Poisson distribution to model the number of claims (Gupta et al. 1996; Stasinopoulos and Rigby 2007).

In our case, there is just a slight chance that past-week precipitation affects the current-week insurance claims. Hence, we will still keep the current precipitation and additionally explore the lagged effects, using the cross-correlation function (Figure 9.8).

Code
par(mar = c(4, 5, 1, 1) + 0.1, mgp = c(3, 1, 0), mfrow = c(1, 1))
logconstant <- 1
with(Insurance,
     ccf(Precipitation, log(Claims + logconstant), las = 1, lag.max = 3)
)

Figure 9.8: Estimated cross-correlation function (CCF) of time series of the number of home insurance claims and precipitation.

Based on the estimated CCFs (Figure 9.8), past-week precipitation is significantly correlated with the current-week number of claims, so we can add the lagged predictor into our models.

Code
Insurance <- Insurance %>%
    mutate(Precipitation_lag1 = dplyr::lag(Precipitation, 1),
           Week = 1:nrow(Insurance),
           Year = rep(2002:2011, each = 52),
           Claims_ln = log(Claims + logconstant))

Based on Figure 9.9, there might be an increasing trend in the number of claims that we might be able to approximate with a linear function.

Code
p1 <- ggplot2::autoplot(as.ts(log(Insurance$Claims + logconstant))) +
    xlab("Week") +
    ylab("ln(Number of claims)")
p2 <- forecast::ggAcf(as.ts(log(Insurance$Claims + logconstant)),
                      lag.max = 110) +
    ggtitle("") +
    xlab("Lag (weeks)")
p1 + p2 +
    plot_annotation(tag_levels = 'A')

Figure 9.9: Time series plot and sample ACF of the weekly number of claims in a city, after the ln transformation.

Plot the data once again after the transformations (Figure 9.10).

Code
Insurance %>%
    dplyr::select(-Claims, -Year) %>%
    GGally::ggpairs()

Figure 9.10: Scatterplot matrix of the weekly number of weather-related home insurance claims and precipitation.

Fit a GARMA model relating the weekly number of insurance claims to the total precipitation during that and previous weeks.

# The model function doesn't accept NAs, so remove them
Insurance_noNA <- na.omit(Insurance)

library(gamlss.util)
m00zip <- garmaFit(Claims ~ Precipitation + Week + Precipitation_lag1
                   ,family = ZIP
                   ,data = Insurance_noNA)
#> deviance of linear model=  3014

Obtain ACF and PACF plots of the model residuals to select ARMA order (Figure 9.11).

Code
p1 <- forecast::ggAcf(m00zip$residuals) +
    ggtitle("") +
    xlab("Lag (weeks)")
p2 <- forecast::ggAcf(m00zip$residuals, type = "partial") +
    ggtitle("") +
    xlab("Lag (weeks)")
p1 + p2 +
    plot_annotation(tag_levels = 'A')

Figure 9.11: ACF and PACF plots of residuals of the base model GARMA(0,0) based on ZIP distribution.

Based on the observed ACF and PACF patterns in Figure 9.11, an appropriate model for the temporal dependence could be ARMA(3,0). Refit the GARMA model specifying these orders. Then verify that the temporal dependence in residuals was removed (Figure 9.12), and assess other assumptions (Figure 9.13), including homogeneity and normality of the quantile residuals.

set.seed(12345)
m30zip <- garmaFit(Claims ~ Precipitation + Week + Precipitation_lag1
                ,order = c(3, 0)
                ,family = ZIP
                ,data = Insurance_noNA)
#> deviance of linear model=  3014 
#> deviance of  garma model=  2926
summary(m30zip)
#> 
#> Family:  c("ZIP", "Poisson Zero Inflated") 
#> Fitting method: "nlminb" 
#> 
#> Call:  garmaFit(formula = Claims ~ Precipitation + Week + Precipitation_lag1,  
#>     order = c(3, 0), data = Insurance_noNA, family = ZIP) 
#> 
#> 
#> Coefficient(s):
#>                            Estimate  Std. Error  t value   Pr(>|t|)    
#> beta.(Intercept)        0.848144482 0.208730902  4.06334 4.8376e-05 ***
#> beta.Precipitation      0.033050327 0.001415750 23.34475 < 2.22e-16 ***
#> beta.Week               0.000915048 0.000607178  1.50705  0.1317975    
#> beta.Precipitation_lag1 0.017806845 0.001834035  9.70911 < 2.22e-16 ***
#> phi1                    0.308599336 0.027913881 11.05541 < 2.22e-16 ***
#> phi2                    0.038617209 0.024183455  1.59684  0.1103005    
#> phi3                    0.304474331 0.029638021 10.27310 < 2.22e-16 ***
#> sigma                   0.074047092 0.021057484  3.51643  0.0004374 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#>  Degrees of Freedom for the fit: 8 Residual Deg. of Freedom   511 
#> Global Deviance:     2926 
#>             AIC:     2942 
#>             SBC:     2976
Code
p1 <- forecast::ggAcf(m30zip$residuals) +
    ggtitle("") +
    xlab("Lag (weeks)")
p2 <- forecast::ggAcf(m30zip$residuals, type = "partial") +
    ggtitle("") +
    xlab("Lag (weeks)")
p1 + p2 +
    plot_annotation(tag_levels = 'A')

Figure 9.12: ACF and PACF plots of the GARMA(0,3) model residuals based on ZIP distribution.

Code
plot(m30zip)
#> ******************************************************************
#>   Summary of the Randomised Quantile Residuals
#>                            mean   =  0.257 
#>                        variance   =  1.98 
#>                coef. of skewness  =  1.23 
#>                coef. of kurtosis  =  6.76 
#> Filliben correlation coefficient  =  0.967 
#> ******************************************************************

Figure 9.13: Default diagnostics of the GARMA(0,3) model residuals based on ZIP distribution.

See Dunn and Smyth (1996) for the details on randomized quantile residuals. Overall, their poor correspondence with the standard normal distribution shows a lack of fit of the model. See ?gamlss.family for other distribution families, continuous and discrete; somewhat out-of-date tables with many of these distributions listed are available from Stasinopoulos and Rigby (2007).

Here we try one other distribution appropriate for modeling overdispersed count data – negative binomial distribution. See the model summary below and the verification of residuals in Figure 9.14 and Figure 9.15.

set.seed(12345)
m03nbi <- garmaFit(Claims ~ Precipitation + Week + Precipitation_lag1
                ,order = c(0, 3)
                ,family = NBI
                ,data = Insurance_noNA)
#> deviance of linear model=  2324 
#> deviance of  garma model=  2320
summary(m03nbi)
#> 
#> Family:  c("NBI", "Negative Binomial type I") 
#> Fitting method: "nlminb" 
#> 
#> Call:  garmaFit(formula = Claims ~ Precipitation + Week + Precipitation_lag1,  
#>     order = c(0, 3), data = Insurance_noNA, family = NBI) 
#> 
#> 
#> Coefficient(s):
#>                             Estimate   Std. Error  t value   Pr(>|t|)    
#> beta.(Intercept)         0.572171010  0.105838165  5.40609 6.4414e-08 ***
#> beta.Precipitation       0.030544133  0.003048269 10.02016 < 2.22e-16 ***
#> beta.Week                0.001447954  0.000293054  4.94092 7.7755e-07 ***
#> beta.Precipitation_lag1  0.003857115  0.003396527  1.13561 0.25612163    
#> theta1                   0.107102854  0.036155734  2.96226 0.00305385 ** 
#> theta2                   0.115018618  0.030764826  3.73864 0.00018502 ***
#> theta3                  -0.064511562  0.031249621 -2.06440 0.03898028 *  
#> sigma                    0.347744482  0.037636402  9.23958 < 2.22e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#>  Degrees of Freedom for the fit: 8 Residual Deg. of Freedom   511 
#> Global Deviance:     2320 
#>             AIC:     2336 
#>             SBC:     2370
Code
p1 <- forecast::ggAcf(m03nbi$residuals) +
    ggtitle("") +
    xlab("Lag (weeks)")
p2 <- forecast::ggAcf(m03nbi$residuals, type = "partial") +
    ggtitle("") +
    xlab("Lag (weeks)")
p1 + p2 +
    plot_annotation(tag_levels = 'A')

Figure 9.14: ACF and PACF plots of the GARMA(0,3) model residuals based on NBI distribution.

Code
plot(m03nbi)
#> ******************************************************************
#>   Summary of the Randomised Quantile Residuals
#>                            mean   =  0.0133 
#>                        variance   =  1.06 
#>                coef. of skewness  =  0.682 
#>                coef. of kurtosis  =  7.24 
#> Filliben correlation coefficient  =  0.979 
#> ******************************************************************

Figure 9.15: Default diagnostics of the GARMA(0,3) model residuals based on NBI distribution.

The residual diagnostics look better for the latter model. One could also consider modeling the strictly periodical component such as using the Fourier series, however, Figure 9.9 did not show a prominent seasonality.

9.6 GAMLSS

Stasinopoulos and Rigby (2007) provide an extension of a generalized additive model to \(k=1,2,3,4\) parameters \(\boldsymbol{\theta}_k\) of a distribution in a so-called generalized additive model for location scale and shape (GAMLSS). The \(k\) parameters represent the location parameter \(\mu\) (it is what we typically model with regression models), scale \(\sigma\), and two shape parameters: skewness and kurtosis. The model can be further generalized for \(k>4\) if needed. It allows us to fit \(k\) individual models to study relationships between regressors \(\boldsymbol{x}\) and parameters of the response distribution: \[ g_k(\boldsymbol{\theta}_k) = h_k\left(\boldsymbol{X}_k,\boldsymbol{\beta}_k\right) + \sum_{j=1}^{J_k}h_{jk}(\boldsymbol{x}_{jk}), \tag{9.13}\] where \(k=1\) produces model for the mean; \(h_k(\cdot)\) and \(h_{jk}(\cdot)\) are nonlinear functions; \(\boldsymbol{\beta}_k\) is a parameter vector of length \(J_k\); \(\boldsymbol{X}_k\) is an \(n\times J_k\) design matrix; \(\boldsymbol{x}_{jk}\) are vectors of length \(n\). The terms in the GAMLSS provide a flexible framework to specify nonlinearities, random effects, and correlation structure as in the mixed effects models (Zuur et al. 2009); see Table 3 by Stasinopoulos and Rigby (2007) for the possible specifications of the additive terms. Hence, a model of the form Equation 9.13 may accommodate non-normal distributions, possibly nonlinear relationships, and spatiotemporal dependencies in the data.

Example: Insurance claims GAMLSS

Here, we use insights from the latest GARMA model and specify the same regressors and distribution family of the response variable in a GAMLSS.

Negative binomial distribution has two parameters (see ?NBI) – location and scale – so the GAMLSS using this distribution family can include up to two equations (\(k = 1, 2\) in Equation 9.13).

We will keep a linear relationship between claims and the week number (parametric linear trend; note that the variable Week here is the time index, not the week of the year) but will use nonparametric additive smooths for the relationships between number of claims and precipitation amounts.

We will model the scale (variability) of the number of claims using a smooth term of the week number.

We start by fitting a model as follows: \[ \begin{split} Claims_t &= NegBin(\mu_t, \sigma_t) \\ \ln(\mu_t) &= a_0 + a_1 Week_t + f_1(Precipitation_t) + f_2(Precipitation_{t-1}) + \epsilon_t \\ \ln(\sigma_t) &= b_0 + f_3(Week) \\ \end{split} \tag{9.14}\] where \(\epsilon_t \sim \mathrm{WN}(0,\sigma^2)\); \(a_0\), \(a_1\), and \(b_0\) are parametric coefficients; \(f_1\), \(f_2\), and \(f_3\) are nonparametric smooths.

In its expandable collection of smoothers, the R package gamlss features penalized B-splines. See the help files ?gamlss and ?pb for more details and the review of spline functions in R by Perperoglou et al. (2019). However, we used the original P-splines ps() because they provided more visually smooth results than pb() under the default settings. Note that the model summary below has a table for each parameter of the distribution. The obtained term plots are in Figure 9.16 and Figure 9.17.

library(gamlss)
set.seed(12345)
m00_gamlss <- gamlss(Claims ~ ps(Precipitation) + Week + ps(Precipitation_lag1)
                     ,sigma.formula = ~ps(Week)
                     ,family = NBI
                     ,control = gamlss.control(c.crit = 0.01, trace = FALSE)
                     ,data = Insurance_noNA)
summary(m00_gamlss)
#> ******************************************************************
#> Family:  c("NBI", "Negative Binomial type I") 
#> 
#> Call:  gamlss(formula = Claims ~ ps(Precipitation) + Week +  
#>     ps(Precipitation_lag1), sigma.formula = ~ps(Week),  
#>     family = NBI, data = Insurance_noNA, control = gamlss.control(c.crit = 0.01,  
#>         trace = FALSE)) 
#> 
#> Fitting method: RS() 
#> 
#> ------------------------------------------------------------------
#> Mu link function:  log
#> Mu Coefficients:
#>                        Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)            0.572497   0.092566    6.18  1.3e-09 ***
#> ps(Precipitation)      0.014442   0.002691    5.37  1.2e-07 ***
#> Week                   0.001520   0.000269    5.64  2.8e-08 ***
#> ps(Precipitation_lag1) 0.011326   0.002908    3.90  0.00011 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> ------------------------------------------------------------------
#> Sigma link function:  log
#> Sigma Coefficients:
#>              Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) -0.371642   0.218617   -1.70  0.08975 .  
#> ps(Week)    -0.002379   0.000717   -3.32  0.00098 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> ------------------------------------------------------------------
#> NOTE: Additive smoothing terms exist in the formulas: 
#>  i) Std. Error for smoothers are for the linear effect only. 
#> ii) Std. Error for the linear terms maybe are not accurate. 
#> ------------------------------------------------------------------
#> No. of observations in the fit:  519 
#> Degrees of Freedom for the fit:  15
#>       Residual Deg. of Freedom:  504 
#>                       at cycle:  6 
#>  
#> Global Deviance:     2214 
#>             AIC:     2244 
#>             SBC:     2308 
#> ******************************************************************
Code
gamlss.ggplots::fitted_terms(m00_gamlss, rug = TRUE, nrow = 1, what = "mu")

Figure 9.16: GAMLSS terms showing the estimated relationships between the regressors and the location parameter for the distribution of the number of home insurance claims.

Code
gamlss.ggplots::fitted_terms(m00_gamlss, rug = TRUE, nrow = 1, what = "sigma")

Figure 9.17: GAMLSS terms showing the estimated relationships between the regressors and the scale parameter for the distribution of the number of home insurance claims.

For the correlation estimates to work, we need to specify a grouping factor for the random effects. To create a grouping factor, we added a variable with the city ID; here it has only one level "City A" and hence does not affect the estimates substantially. If we had information from multiple cities, the specified form of autoregressive structure form = ~Week|City could readily accommodate it.

The code below estimates the model from Equation 9.14 again but assumes the new autocorrelation structure in the residuals: \(\epsilon_t \sim\) ARMA(0,3). The control arguments change the default settings to speed up the algorithm convergence. See the model summary below and the verification of residuals in Figure 9.18.

set.seed(12345)
Insurance_noNA$City <- as.factor("City A")
m03_gamlss <- gamlss(Claims ~ re(fixed = ~ps(Precipitation) + Week + ps(Precipitation_lag1)
                                 ,random = ~1|City
                                 ,correlation = corARMA(form = ~Week|City, q = 3)
                                 ,method = "REML")
                     ,sigma.formula = ~ps(Week)
                     ,family = NBI
                     ,i.control = glim.control(cc = 0.01, bf.cyc = 100, bf.tol = 0.01)
                     ,control = gamlss.control(c.crit = 0.01, trace = FALSE)
                     ,data = Insurance_noNA)

Model summary for the location parameter:

summary(getSmo(m03_gamlss))
#> Linear mixed-effects model fit by REML
#>   Data: Data 
#>    AIC  BIC logLik
#>   1521 1559   -751
#> 
#> Random effects:
#>  Formula: ~1 | City
#>         (Intercept) Residual
#> StdDev:       0.147     1.26
#> 
#> Correlation Structure: ARMA(0,3)
#>  Formula: ~Week | City 
#>  Parameter estimate(s):
#> Theta1 Theta2 Theta3 
#> 0.1946 0.0437 0.0332 
#> Variance function:
#>  Structure: fixed weights
#>  Formula: ~W.var 
#> Fixed effects:  list(fix.formula) 
#>                         Value Std.Error  DF t-value p-value
#> (Intercept)            -0.568    0.2051 515   -2.77  0.0058
#> ps(Precipitation)       0.018    0.0033 515    5.49  0.0000
#> Week                    0.001    0.0004 515    3.36  0.0008
#> ps(Precipitation_lag1)  0.009    0.0036 515    2.64  0.0086
#>  Correlation: 
#>                        (Intr) ps(Pr) Week  
#> ps(Precipitation)      -0.145              
#> Week                   -0.616 -0.010       
#> ps(Precipitation_lag1) -0.135  0.017 -0.022
#> 
#> Standardized Within-Group Residuals:
#>    Min     Q1    Med     Q3    Max 
#> -1.384 -0.549 -0.155  0.327 14.056 
#> 
#> Number of Observations: 519
#> Number of Groups: 1

Model summary for all distribution parameters:

summary(m03_gamlss)
#> ******************************************************************
#> Family:  c("NBI", "Negative Binomial type I") 
#> 
#> Call:  gamlss(formula = Claims ~ re(fixed = ~ps(Precipitation) +  
#>     Week + ps(Precipitation_lag1), random = ~1 | City,  
#>     correlation = corARMA(form = ~Week | City, q = 3),  
#>     method = "REML"), sigma.formula = ~ps(Week), family = NBI,  
#>     data = Insurance_noNA, control = gamlss.control(c.crit = 0.01,  
#>         trace = FALSE), i.control = glim.control(cc = 0.01,  
#>         bf.cyc = 100, bf.tol = 0.01)) 
#> 
#> Fitting method: RS() 
#> 
#> ------------------------------------------------------------------
#> Mu link function:  log
#> Mu Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)   1.1723     0.0329    35.6   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> ------------------------------------------------------------------
#> Sigma link function:  log
#> Sigma Coefficients:
#>              Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)  0.115810   0.201071    0.58     0.56    
#> ps(Week)    -0.003421   0.000684   -5.00  7.8e-07 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> ------------------------------------------------------------------
#> NOTE: Additive smoothing terms exist in the formulas: 
#>  i) Std. Error for smoothers are for the linear effect only. 
#> ii) Std. Error for the linear terms maybe are not accurate. 
#> ------------------------------------------------------------------
#> No. of observations in the fit:  519 
#> Degrees of Freedom for the fit:  9
#>       Residual Deg. of Freedom:  510 
#>                       at cycle:  5 
#>  
#> Global Deviance:     2240 
#>             AIC:     2258 
#>             SBC:     2296 
#> ******************************************************************
Code
plot(m03_gamlss, ts = TRUE)
#> ******************************************************************
#>   Summary of the Randomised Quantile Residuals
#>                            mean   =  0.0141 
#>                        variance   =  0.924 
#>                coef. of skewness  =  0.446 
#>                coef. of kurtosis  =  5.68 
#> Filliben correlation coefficient  =  0.987 
#> ******************************************************************

Figure 9.18: Residual diagnostics of the GAMLSS for the number of home insurance claims.

Hence, compared with the GARMA model from the previous section, the GAMLSS Equation 9.14 uses the same predictors and distribution family and specifies ARMA(0,3) dependence in the residuals. What differs is that the GAMLSS allows nonlinear relationships between the number of claims and precipitation and models the variability changing nonlinearly across weeks.

9.7 Granger causality

The Granger causality (Granger 1969; Kirchgässner and Wolters 2007) concept is based on predictability, which is why we should consider it in the time series course. Pearl causality is based on the analysis of interventions (Rebane and Pearl 1987; Pearl 2009).

Let \(I_t\) be the total information set available at the time \(t\). This information set includes the two time series \(X\) and \(Y\). Let \(\bar{X}_t\) be the set of all current and past values of \(X\), i.e., \(\bar{X}_t = \{X_{t}, X_{t-1}, \dots, X_{t-k}, \dots \}\) and analogously of \(Y\). Let \(\sigma^2(\cdot)\) be the variance of the corresponding forecast error.

Note

Difference of two sets, \(A\) and \(B\), is denoted by \(A \setminus B\); but sometimes the minus sign is used, \(A - B\).

Granger causality

\(X\) is (simply) Granger causal to \(Y\) if future values of \(Y\) can be predicted better, i.e., with a smaller forecast error variance, if current and past values of \(X\) are used: \[ \sigma^2(Y_{t+1}|I_t) < \sigma^2(Y_{t+1}|I_t \setminus \bar{X}_t). \tag{9.15}\]

Instantaneous Granger causality

\(X\) is instantaneously Granger causal to \(Y\) if the future value of \(Y\), \(Y_{t+1}\), can be predicted better, i.e., with a smaller forecast error variance, if the future value of \(X\), \(X_{t+1}\), is used in addition to the current and past values of \(X\): \[ \sigma^2(Y_{t+1}|\{I_t, X_{t+1}\}) < \sigma^2(Y_{t+1}|I_t ). \tag{9.16}\]

Feedback

There is feedback between \(X\) and \(Y\) if \(X\) is causal to \(Y\) and \(Y\) is causal to \(X\). Feedback is only defined for the case of simple causal relations.

The test for Equation 9.15 and Equation 9.16 is, essentially, an \(F\)-test comparing two nested models: with additional predictors \(X\) and without. In other words, consider the model: \[ Y_t = \beta_0 + \sum_{k=1}^{k_1}\beta_k Y_{t-k} + \sum_{k=k_0}^{k_2}\alpha_k X_{t-k} + U_t \tag{9.17}\] with \(k_0 = 1\). An \(F\)-test is applied to test the null hypothesis, H\(_0\): \(\alpha_1 = \alpha_2 = \dots = \alpha_{k_2} = 0\). By switching \(X\) and \(Y\) in Equation 9.17, it can be tested whether a simple causal relation from \(Y\) to \(X\) exists. There is a feedback relation if the null hypothesis is rejected in both directions (\(X\rightarrow Y\) and \(Y\rightarrow X\)). To test whether there is an instantaneous causality, we finally set \(k_0 = 0\) and perform a \(t\) or \(F\)-test for the null hypothesis H\(_0\): \(\alpha_0 = 0\).

The problem with this test is that the results are strongly dependent on the number of lags of the explanatory variable, \(k_2\). There is a trade-off: the more lagged values we include, the better the influence of this variable can be captured. This argues for a high maximal lag. On the other hand, the power of this test is lower the more lagged values are included (Chapter 3 of Kirchgässner and Wolters 2007). Two general procedures can be used to select the lags: inspecting the sensitivity of results to different \(k_2\) (sensitivity analysis) or one of the different information criteria guiding model selection.

Example: Insurance claims and precipitation Granger causality test

For example, use the insurance data to test the relationships between the log-transformed home insurance number of claims and precipitation. A quick test has been performed to check that the time series are stationary and do not have a strong seasonality, so the chance of detecting spurious relationships is minimized. We can use the series in Equation 9.17.

lmtest::grangertest(Claims_ln ~ Precipitation 
                    ,order = 1
                    ,data = Insurance_noNA)
#> Granger causality test
#> 
#> Model 1: Claims_ln ~ Lags(Claims_ln, 1:1) + Lags(Precipitation, 1:1)
#> Model 2: Claims_ln ~ Lags(Claims_ln, 1:1)
#>   Res.Df Df    F Pr(>F)   
#> 1    515                  
#> 2    516 -1 10.5 0.0013 **
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The low \(p\)-value shows that precipitation is a Granger cause of the number of home insurance claims. Now test the reverse relationship.

lmtest::grangertest(Precipitation ~ Claims_ln  
                    ,order = 1
                    ,data = Insurance_noNA)
#> Granger causality test
#> 
#> Model 1: Precipitation ~ Lags(Precipitation, 1:1) + Lags(Claims_ln, 1:1)
#> Model 2: Precipitation ~ Lags(Precipitation, 1:1)
#>   Res.Df Df   F Pr(>F)
#> 1    515              
#> 2    516 -1 0.2   0.65

Reverse testing does not confirm a statistically significant Granger causality. Hence, we do not have enough evidence to claim that insurance claims are a Granger cause of precipitation (we could expect to come to this conclusion based on our knowledge of how things work), and hence there is no evidence of feedback between losses and precipitation.

The function lmtest::grangertest() does not allow us to set order = 0 (to test instantaneous Granger causality), but we can do it manually. First, to show that ‘manual’ results match the lmtest::grangertest() output, repeat the test above using two nested models with lag 1.

M1 <- lm(Claims_ln ~ dplyr::lag(Claims_ln, 1) + dplyr::lag(Precipitation, 1)
         ,data = Insurance_noNA)
M2 <- lm(Claims_ln ~ dplyr::lag(Claims_ln, 1)
         ,data = Insurance_noNA)
anova(M1, M2)
#> Analysis of Variance Table
#> 
#> Model 1: Claims_ln ~ dplyr::lag(Claims_ln, 1) + dplyr::lag(Precipitation, 
#>     1)
#> Model 2: Claims_ln ~ dplyr::lag(Claims_ln, 1)
#>   Res.Df RSS Df Sum of Sq    F Pr(>F)   
#> 1    515 211                            
#> 2    516 215 -1     -4.32 10.5 0.0013 **
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The results match.

Second, test the instantaneous Granger causality in the same manner.

M3 <- lm(Claims_ln ~ dplyr::lag(Claims_ln, 1) + dplyr::lag(Precipitation, 1) + 
             Precipitation, data = Insurance_noNA)
M4 <- lm(Claims_ln ~ dplyr::lag(Claims_ln, 1) + dplyr::lag(Precipitation, 1)
         ,data = Insurance_noNA)
anova(M3, M4)
#> Analysis of Variance Table
#> 
#> Model 1: Claims_ln ~ dplyr::lag(Claims_ln, 1) + dplyr::lag(Precipitation, 
#>     1) + Precipitation
#> Model 2: Claims_ln ~ dplyr::lag(Claims_ln, 1) + dplyr::lag(Precipitation, 
#>     1)
#>   Res.Df RSS Df Sum of Sq  F  Pr(>F)    
#> 1    514 203                            
#> 2    515 211 -1     -7.91 20 9.5e-06 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The results show the presence of such causality.

As an extension to the demonstrated techniques for testing Granger causality, we may consider more complex generalized and additive models, to relax the assumptions of normality and linearity in the modeling process.

Note

The lmtest::grangertest() options set one value to both \(k_1\) and \(k_2\) in Equation 9.17. In our example, it was \(k_1 = k_2 = 1\). The ‘manual’ test using the function anova() can be used for models with \(k_1 = k_2\) or \(k_1 \neq k_2\).

9.8 About predictions

Let \(\hat{Y}_T(h)\) be a forecast \(h\) steps ahead made at the time \(T\). If \(\hat{Y}_T(h)\) only uses information up to time \(T\), the resulting forecasts are called out-of-sample forecasts. Economists call them ex-ante forecasts. We have discussed several ways to select the optimal method or model for forecasting, e.g., using PMAE, PMSE, or coverage – all calculated on a testing set. Chatfield (2000) mentions several ways to unfairly ‘improve’ forecasts:

  1. Fitting the model to all the data including the test set.
  2. Fitting several models to the training set and choosing the model which gives the best ‘forecasts’ of the test set. The selected model is then used (again) to produce forecasts of the test set, even though the latter has already been used in the modeling process.
  3. Using the known test-set values of ‘future’ observations on the explanatory variables in multivariate forecasting. This will improve forecasts of the dependent variable in the test set, but these future values will not of course be known at the time the forecast is supposedly made (though in practice the ‘forecast’ is made at a later date). Economists call such forecasts ex-post forecasts to distinguish them from ex-ante forecasts. The latter, being genuinely out-of-sample, use forecasts of future values of explanatory variables, where necessary, to compute forecasts of the response variable. Ex-post forecasts can be useful for assessing the effects of explanatory variables, provided the analyst does not pretend that they are genuine out-of-sample forecasts.

So what to do if we put lots of effort to build a regression model using time series and need to forecast the response, \(Y_t\), which is modeled using different independent variables \(X_{t,k}\) (\(k=1,\dots,K\))? Two options are possible.

Leading indicators

If \(X_{t,k}\)’s are leading indicators with lags starting at \(l\), we, generally, would not need their future values to obtain the forecasts \(\hat{Y}_T(h)\), where \(h\leqslant l\). For example, the model for losses tested in Section 9.7 shows that precipitation with lag 1 is a good predictor for current losses, i.e., precipitation is a leading indicator. The 1-week ahead forecast of \(Y_{t+1}\) can be obtained using the current precipitation \(X_t\) (all data are available). If \(h>l\), we will be forced to forecast the independent variables, \(X_{t,k}\)’s – see the next option.

Forecast of predictors

If we opt for forecasting \(X_{t,k}\)’s, the errors (uncertainty) of such forecasts will be larger, because future \(X_{t,k}\)’s themselves will be the estimates. Nevertheless, it might be the only choice when leading indicators are not available. Building a full and comprehensive model with all diagnostics for each regressor is usually unfeasible and even problematic if we plan to consider multivariate models for regressors (the complexity of models will quickly escalate). As an alternative, it is common to use automatic or semi-automatic univariate procedures that can help to forecast each of the \(X_{t,k}\)’s. For example, consider exponential smoothing, Holt–Winters smoothing, and auto-selected SARIMA/ARIMA/ARMA/AR/MA models – all those can be automated for a large number of forecasts to make.

9.9 Conclusion

Multivariate models are still much more difficult to fit than univariate ones. Multiple regression remains a treacherous procedure when applied to time series data. Many observed time series exhibit nonlinear characteristics, but nonlinear models often fail to give better out-of-sample forecasts than linear models, perhaps because the latter are more robust to departures from model assumptions. It is always a good idea to end with the so-called eyeball test. Plot the forecasts on a time plot of the data and check that they look intuitively reasonable (Chatfield 2000).